UniRx: TakeUntil

TakeUntil は引数で渡した IObservable が最初のデータを通知したら、自身の通知をそこで終了させるオペレータです。

以下のサンプルは、1 秒ごとにデータを通知しますが、スペースキーが押されると、そこで通知を終了します。

using System;
using UniRx;
using UniRx.Diagnostics;
using UnityEngine;

public class Main : MonoBehaviour
{
    private Subject<Unit> _subject;
    
    void Start()
    {
        _subject = new Subject<Unit>();

        var s = Observable
            .Interval(TimeSpan.FromSeconds(1))
            .TakeUntil(_subject);
        s.Debug().Subscribe();
    }
    
    void Update()
    {
        // スペースキーを押すと、データ通知
        if (Input.GetKeyDown(KeyCode.Space))
        {
            Debug.Log("スペースキーを押しました");
            _subject.OnNext(Unit.Default);
            _subject.OnCompleted();            
        }
    }        
}

実行結果です。

[18:20:19:830] OnSubscribe
[18:20:21:037] OnNext(0)
[18:20:22:047] OnNext(1)
[18:20:23:063] OnNext(2)
[18:20:24:070] OnNext(3)
[18:20:24:417] スペースキーを押しました
[18:20:24:419] OnCompleted()

スペースキーを押すと、OnCompleted が呼ばれているのが確認できます。

RxJava には通知データを元に終了判定を行うオーバーロードがある

RxJava の takeUntil メソッド には、引数に述語関数を渡して、通知データを元に通知を終了するかを判定するオーバーロードが定義されています。

UniRx には実装が見当たらなかったので、自作してみました。

using System;
using UniRx;

public static class ObservableExtensions
{
    public static IObservable<T> TakeUntil<T>(this IObservable<T> source, Predicate<T> stopPredicate)
    {
        bool stopValueFound = false;
        T stopValue = default;
        var s = source.TakeWhile(e =>
        {
            if (stopPredicate(e))
            {
                stopValueFound = true;
                stopValue = e;
                return false;
            }
            return true;
        });

        return s.Concat(Observable.Create<T>(observer =>
        {
            if (stopValueFound) observer.OnNext(stopValue);
            observer.OnCompleted();
            return Disposable.Empty;
        }));
    }    
}

TakeWhile で stopPredicate が true になるかをチェックします。 もし true になる場合は、その値を Concat で末尾に加えています。

お試しコード:

using UniRx;
using UniRx.Diagnostics;
using UnityEngine;

public class Main : MonoBehaviour
{
    void Start()
    {        
        // 偶数が流れてくるまでデータ通知
        var s = new[] { 1, 3, 5, 10, 2, 9, 0 }
            .ToObservable()
            .TakeUntil(e => e % 2 == 0);
        s.Debug().Subscribe();
        
        // 条件にマッチしないなら全てのデータを通知
        var t = Observable.Range(1, 3)
            .TakeUntil(e => e > 10);
        t.Debug().Subscribe();
    }    
}

実行結果です。

OnSubscribe
OnNext(1)
OnNext(3)
OnNext(5)
OnNext(10) // 偶数が流れてきたので、ここで通知を終了する
OnCompleted()
OnSubscribe
OnNext(1)
OnNext(2)
OnNext(3)
OnCompleted()

参考

• ReactiveX - TakeUntil operator

UniRx: Take と First と Single

Take, First, Single の各オペレータは、ストリームに流れる値を取り出します。 オペレータに応じて、それぞれストリームにいくつ値がながれるか、期待する個数が異なります。

• Take は、ストリームの最初の N 個を取り出します(N は引数で指定)。不足があっても構いません。
• First は、ストリームの最初の値を取り出します。ストリームには、ひとつ以上の値が流れることを期待します。
• Single は、ストリームの最初の値を取り出します。ストリームには、ちょうどひとつだけ値が流れることを期待します。

Take のサンプル

void Start()
{
    var s = Observable.Range(1, 3);
    s.Take(2).Debug().Subscribe(); // 2 個取り出す
    s.Take(5).Debug().Subscribe(); // 5 個取り出す
}

実行結果です。

OnSubscribe
OnNext(1)
OnNext(2)
OnCompleted()
OnSubscribe
OnNext(1)
OnNext(2)
OnNext(3)
OnCompleted()

Take() は引数で指定された個数だけ値を取り出しますが、不足分があっても構いません。

First のサンプル

void Start()
{
    var s = Observable.Range(1, 3).First();
    s.Debug().Subscribe();
}

実行結果です。

OnSubscribe
OnNext(1)
OnCompleted()

• もし、ストリームに値が流れない場合は、「InvalidOperationException: sequence is empty」例外が生成されます。

Single のサンプル

void Start()
{
    var s = Observable.Return(100).Single();
    s.Debug().Subscribe();
}

実行結果です。

OnSubscribe
OnNext(100)
OnCompleted()

• もし、ストリームに値が流れない場合は、「InvalidOperationException: sequence is empty」例外が生成されます。
• もし、ストリームにふたつ以上の値が流れる場合は、「InvalidOperationException: sequence is not single」例外が生成されます。

参考

• ReactiveX - Take operator
• ReactiveX - First operator
• ReactiveX - Single

UniRx: Subject とそれ以外のソースでのストリームの流れを眺める

• Subject にいくつかオペレータを敵賞して Subscribe する場合と
• Subject 以外のたとえば Range にいくつかオペレータを適用して Subscribe する場合

について、Observer にどのようにして値が流れるのか見ていきます。

まずは Subject から。

using System;
using UniRx;
using UnityEngine;

public class Main : MonoBehaviour
{
    private Subject<DateTime> _subject;
    
    void Start()
    {
        _subject = new Subject<DateTime>();
        _subject
            .Select(e => e)
            .Subscribe(e => Debug.Log($"e = {e}"));       
    }

    void Update()
    {
        if (Input.GetKeyDown(KeyCode.Space))
        {
            _subject.OnNext(DateTime.Now);            
        }
    }    
}

Subscribe メソッドを呼ぶと、以下のように処理が進みます。

SelectObservable.Subscribe
  => SelectObservable.SubscribeCore
    => Subject.Subscribe
      => Observer を Subject が内部にもつ ListObserver に登録する

Subject の OnNext を呼びだすと、ListObserver に登録されている Observer の OnNext が呼ばれます。 このようにして Observer に値が通知されます。

次に Range の場合です。

using System;
using UniRx;
using UnityEngine;

public class Main : MonoBehaviour
{    
    void Start()
    {
        Observable.Range(1, 3)
            .Select(e => e)
            .Subscribe(e => Debug.Log($"e = {e}"));
    }
}

Subscribe をメソッドを呼ぶと、以下のように処理が進みます。

SelectObservable.Subscribe
  => SelectObservable.SubscribeCore
    => RangeObservable.Subscribe
      => RangeObservable.SubscribeCore の引数に渡された Observer の OnNext 呼び出す

Range の場合は、Subscribe を呼び出すとストリームに値が流れています。

UniRx: 時間を(複数)指定してイベント発行

下のコードは、1 秒、3 秒、4 秒後にイベントを発行するサンプルです。

using System;
using System.Linq;
using UniRx;
using UniRx.Diagnostics;
using UnityEngine;

public class Main : MonoBehaviour
{
    void Start()
    {
        var fireTimes = new[] { 1, 3, 4 }; // 1 秒, 3 秒, 4 秒後にイベント発行
        var s = fireTimes.Select(e => Observable.Timer(TimeSpan.FromSeconds(e))).Merge();
        s.Debug().Subscribe();
    }
}

実行結果です。

[12:17:05:094] OnSubscribe
[12:17:06:302] OnNext(0)
[12:17:08:287] OnNext(0)
[12:17:09:297] OnNext(0)
[12:17:09:300] OnCompleted()

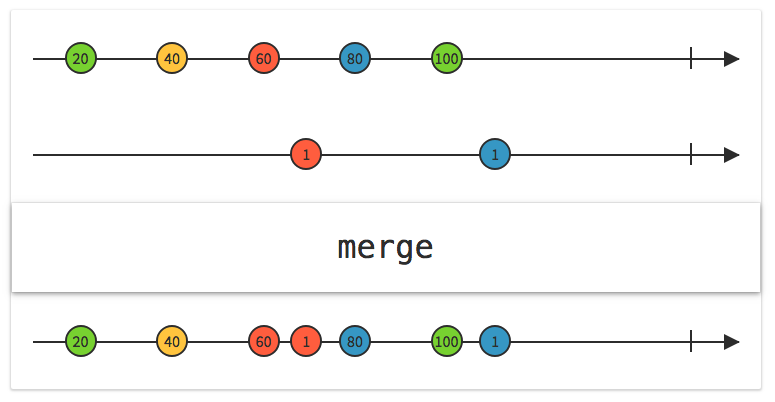
Merge オペレータ

• ReactiveX - Merge operator

一時変数のキャプチャ。C# 5.0 の foreach の破壊的変更

qiita.com

上の記事を読んで、サンプルコードを書いてみました。

using System;
using System.Collections.Generic;
using System.Linq;

class Program
{
    static void Main()
    {
        var a = new List<Action>();
        var b = new List<Action>();
        for (int i = 0; i < 3; i++)
        {
            a.Add(() => Console.WriteLine($"[a] {i}"));

            int x = i;
            b.Add(() => Console.WriteLine($"[b] {x}"));
        }

        var c = new List<Action>();
        foreach (var e in new[] { 0, 1, 2 })
        // or foreach (var e in Enumerable.Range(0, 3))
        {
            c.Add(() => Console.WriteLine($"[c] {e}"));
        }

        foreach (var e in a) e();
        foreach (var e in b) e();
        foreach (var e in c) e();
    }
}

実行結果です。

[a] 3
[a] 3
[a] 3
[b] 0
[b] 1
[b] 2
[c] 0
[c] 1
[c] 2

Task.Run のサンプルです。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Threading.Tasks;

class Program
{
    static void Main()
    {
        var a = new List<Action>();
        foreach (var e in Enumerable.Range(0, 10))
        {
            Task.Run(() => Console.WriteLine(e));
        }
    }
}

実行結果です。

0
1
4
6
3
2
7
5

参考

ufcpp.net

UniRx: Subject への購読とそのキャンセル処理を眺める

Subject クラスへの購読と、その購読のキャンセル処理について以下のサンプルコードで見ていきます。

using UniRx;
using UnityEngine;

public class Main : MonoBehaviour
{
    void Start()
    {
        var subject = new Subject<int>();
        // 購読する
        var disposable = subject.Subscribe();
        // 購読をキャンセルする
        disposable.Dispose();
    }
}

Subject の、

• Subscribe() を呼び出すと、内部でどのような処理が行われるか
• Subscribe() から返される IDisposable の Dispose() を呼び出すと、どのような処理が行われるか

を見ていきます。

Subscribe() メソッドは、拡張メソッドとして定義されています。

public static IDisposable Subscribe<T>(this IObservable<T> source)
{
    return source.Subscribe(UniRx.InternalUtil.ThrowObserver<T>.Instance);
}

次に Subject.Subscribe() が呼ばれます。

public sealed class Subject<T> : ISubject<T>, IDisposable, IOptimizedObservable<T>
{
    public IDisposable Subscribe(IObserver<T> observer)
    {
        if (observer == null) throw new ArgumentNullException("observer");

        var ex = default(Exception);

        lock (observerLock)
        {
            ThrowIfDisposed();
            if (!isStopped)
            {
                var listObserver = outObserver as ListObserver<T>;
                if (listObserver != null)
                {
                    outObserver = listObserver.Add(observer);
                }
                else
                {
                    var current = outObserver;
                    if (current is EmptyObserver<T>)
                    {
                        outObserver = observer;
                    }
                    else
                    {
                        outObserver = new ListObserver<T>(new ImmutableList<IObserver<T>>(new[] { current, observer }));
                    }
                }

                return new Subscription(this, observer);
            }

            ex = lastError;
        }

        if (ex != null)
        {
            observer.OnError(ex);
        }
        else
        {
            observer.OnCompleted();
        }

        return Disposable.Empty;
    }
}

Subject クラス内部で ListObserver という IObserver を格納するためのコンテナを持っており、そのコンテナに引数で渡された observer を格納しています。興味深い特徴として、ListObserver に新たな observer を追加するたびに、新しい ListObserver が作られます。

ListObserver がそのような仕組みになっている理由について、UniRx 作者さんのブログにそれらしい記述を見つけたのですが、自分の理解不足のためかよく理解できませんでした。

次に Subscribe() メソッドの戻り値の Subscription クラスの実装を見てみます。

class Subscription : IDisposable
{
    readonly object gate = new object();
    Subject<T> parent;
    IObserver<T> unsubscribeTarget;

    public Subscription(Subject<T> parent, IObserver<T> unsubscribeTarget)
    {
        this.parent = parent;
        this.unsubscribeTarget = unsubscribeTarget;
    }

    public void Dispose()
    {
        lock (gate)
        {
            if (parent != null)
            {
                lock (parent.observerLock)
                {
                    var listObserver = parent.outObserver as ListObserver<T>;
                    if (listObserver != null)
                    {
                        parent.outObserver = listObserver.Remove(unsubscribeTarget);
                    }
                    else
                    {
                        parent.outObserver = EmptyObserver<T>.Instance;
                    }

                    unsubscribeTarget = null;
                    parent = null;
                }
            }
        }
    }
}

Subscription.Dispose() を呼び出すと、ListObserver に登録した observer が削除される仕組みになっています。

まとめると、以下の処理が行われています。

• Subject.Subscribe(IObserver<T> observer) を呼ぶと、引数の observer を ListObserver に登録
• Subscription の Dispose() を呼ぶと、ListObserver から observer を削除

UniRx: Subject は IObserver であり IObservable でもある

Subject の定義をみると次のようになっています。

public sealed class Subject<T> : ISubject<T>, IDisposable, IOptimizedObservable<T>
{
}

ISubject の定義は、

public interface ISubject<TSource, TResult> : IObserver<TSource>, IObservable<TResult>
{
}

public interface ISubject<T> : ISubject<T, T>, IObserver<T>, IObservable<T>
{
}

となっています。つまり、Subject は IObserver であり、IObservable でもあります。

Subject は、IObserver であるのでストリームにデータを流す(OnNext)ことができます、。

using UniRx;
using UniRx.Diagnostics;
using UnityEngine;

public class Main : MonoBehaviour
{
    void Start()
    {
        var subject = new Subject<int>();
        subject.Debug().Subscribe();

        subject.OnNext(10);
        subject.OnNext(20);
        subject.OnNext(30);
        subject.OnCompleted();        
    }
}

実行結果です。

OnSubscribe
OnNext(10)
OnNext(20)
OnNext(30)
OnCompleted()

また、Subject は、IObservable でもありますので Subscribe の引数に渡すことができます。

using UniRx;
using UnityEngine;

public class Main : MonoBehaviour
{
    void Start()
    {
        var subject = new Subject<int>();
        subject.Debug().Subscribe();

        Observable.Range(1, 3).Subscribe(subject);
    }
}

実行結果です。

OnSubscribe
OnNext(1)
OnNext(2)
OnNext(3)
OnCompleted()